10.2 Graph Terminology

p672

Homework

p687: 23, 24, 25, 52, 53, 54

In Exercises 21–25 determine whether the graph is bipartite. You may find it useful to apply Theorem 4 and answer the question by determining whether it is possible to assign either red or blue to each vertex so that no two adjacent vertices are assigned the same color.
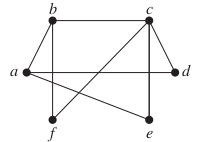
23. Graph

Solution

Not bipartite.

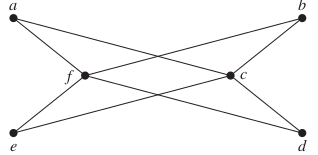
24. Graph

Solution

Bipartite

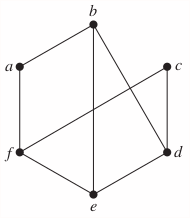
25. Graph

Solution

Not bipartite.

52. Let G be a graph with v vertices and e edges. Let M be the maximum degree of the vertices of G, and let m be the minimum degree of the vertices of G. Show that
a) 2e/v≥m2e/v \geq m   b) 2e/v≤M2e/v \leq M.

Solution

Let the iith vertex be viv_i, and the degree of viv_i be mim_i.

m≤mi≤Mm+m+⋯+m⎵v times≤m1+m2+⋯+mi+⋯+mv≤M+M+⋯+M⎵v timesvm≤∑i∈vdeg(vi)≤vMvm≤2e≤vMThe handshaking theoremm≤2ev≤Ma and b are proved.\begin{aligned} m &\leq m_i\leq M\\ \underbrace{m + m + \cdots + m}_{v \text{ times}} &\leq m_1 + m_2 + \cdots +m_i+ \cdots + m_v \leq \underbrace{M + M + \cdots + M}_{v \text{ times}}\\ vm &\leq \sum_{i\in v}{deg(v_i)} \leq vM\\ vm &\leq 2e \leq vM \quad \text{The handshaking theorem}\\ m &\leq \frac{2e}{v} \leq M \quad \text{a and b are proved.} \end{aligned}

A simple graph is called regular if every vertex of this graph has the same degree. A regular graph is called n-regular if every vertex in this graph has degree n.
53. For which values of n are these graphs regular?
a) KnK_n   b) CnC_n   c) WnW_n   d) QnQ_n

Solution

a. For n≥1n\geq 1, KnK_n is a (n-1)-regular graph.
b. For n≥3n\geq 3, CnC_n is a 2-regular graph.
c. For n=3n=3, WnW_n is a 3-regular graph.
d. For n≥0n \geq 0, WnW_n is a n-regular graph.

54. For which values of m and n is Km,nK_{m,n} regular?

Solution

When m=nm=n, Km,nK_{m,n} is regular.

64. Show that if GG is a bipartite simple graph with vv vertices and ee edges, then e⩽v24e \les \frac{v^2}{4}.

Solution