11.3 Tree Traversal
Preorder
Let be an ordered rooted tree with root . It consists only of , then is the preorder trasversal of . Otherwise, suppose that are the subtrees at from left to right in . The preorder trasveral begins by visiting . It continues by traversing in preorder, then in preorder, and so on, until is traversed in preorder.
Root => Left => Right
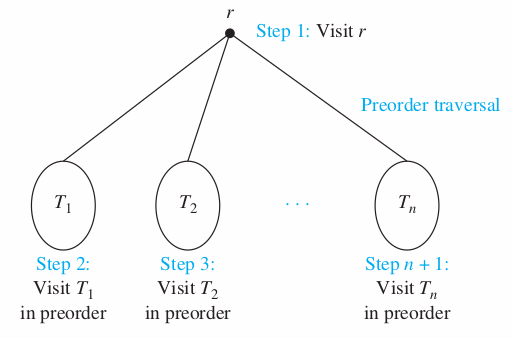
Algorithem 1 Preorder traversal
procedure preorder(T: ordered rooted tree)
r := root of T
list r
for each child c of r from left to right
T(c) := subtree with c as its root
procedure(T(c))
Inorder
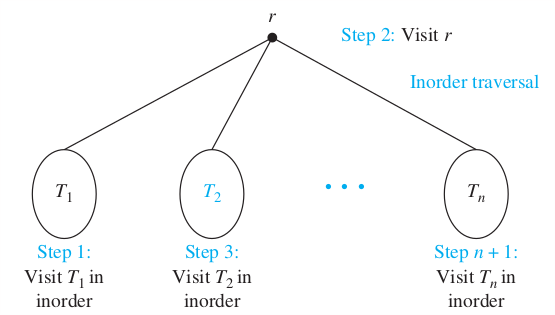
Let be an ordered rooted tree with root . It consists only of , then is the inorder trasversal of . Otherwise, suppose that are the subtrees at from left to right in . The inorder trasveral begins by traversing in inorder, then visiting . It continues by traversing in inorder, then in inorder, ..., and finally in order.
Left => Root => Right
Example
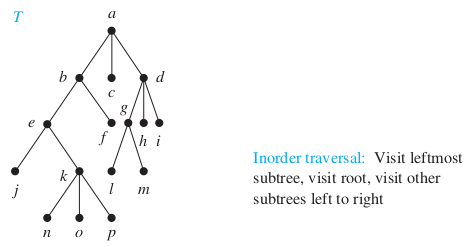
Solution
b, a, c, d
e, b, f, a, c, g, d, h, i
j, e, k, b, f, a, c, l, g, m, d, h, i
j, e, n, k, o, p, b, f, a, c, l, g, m, d, h, i
Algorithem 2 Inorder traversal
procedure inorder(T: ordered rooted tree)
r := root of T
if r is a leaf then list r
else
l := first child of r from left to right
T(l) := subtree with l as its root
inorder(T(l))
list r
for each child c of r except l from left to right
T(c) := subtree with c as its root
inorder(T(c))
Postorder
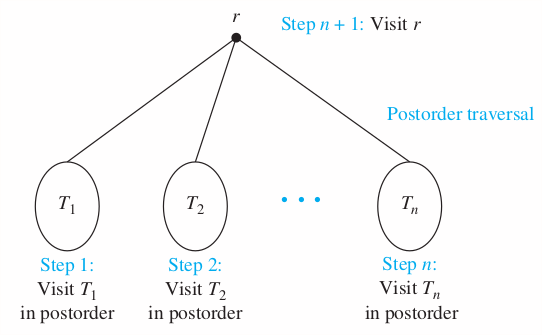
Let be an ordered rooted tree with root . It consists only of , then is the postorder trasversal of . Otherwise, suppose that are the subtrees at from left to right in . The postorder trasveral begins by traversing in postorder, then in postorder, ... then in postorder, and ends by visiting .
Left => Right => Root
Example
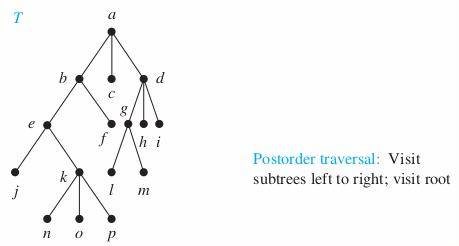
Solution
b, c, d, a
e, f, b, c, g, h, i, d, a
j, k, e, f, b, c, l, m, g, h, i, d, a
j, n, o, p, k, e, f, b, c, l, m, g, h, i, d, a
Algorithem 3 Postorder traversal
procedure postorder(T: ordered rooted tree)
r := root of T
for each child c of r from left to right
T(c) := subtree with c as its root
postorder(T(c))
list r
Homework
p804: 8, 9
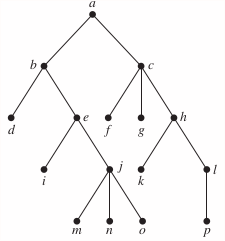
In Exercises 7–9 determine the order in which a preorder traversal visits the vertices of the given ordered rooted tree.
8. 
Solution
a, b, d, e, i, j, m, n, o, c, f, g, h, k, l, p
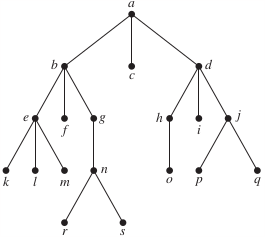
9. 
Solution
a, b, e, k, l, m, f, g, n, r, s, c, d, h, o, i, j, p, q