Algorithm

The algorithm restructures a tree in the way that a link is created between a current node and its predecessor(in a BST) during traversal and is removed later.

Preorder: root -> left -> right

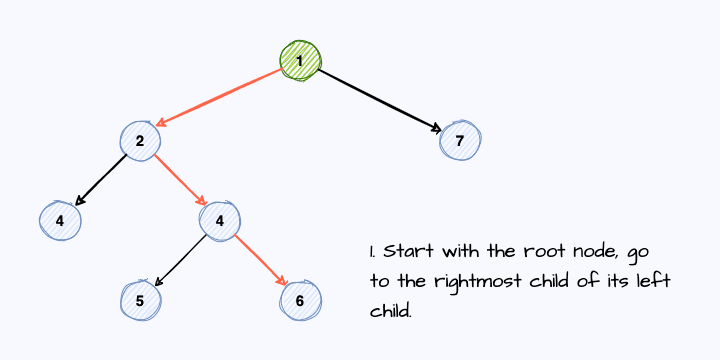
1. Start the traversal with the root node as the current node, go to its left child
2. if the left child
   • 2.1 does not exist, read the current node and move to its right child.
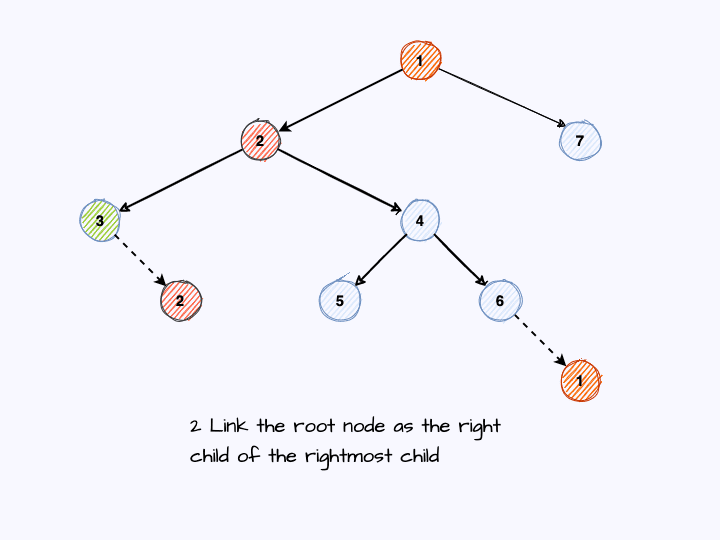
   • 2.2 does exist, find the rightmost child of this left child. For this rightmost child
     • 2.21 if it has not linked to the current node, let the current node be the right child of this rightmost child and read the current node
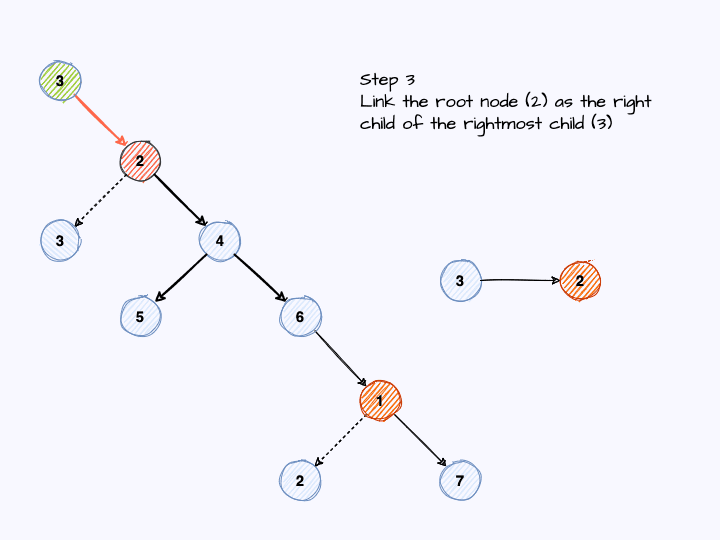
     • 2.22 if the link has been made, namely (rightmost child).right == current node, there is a loop and we need to break the loop by removing the link. Now skip the current node (it’s has already been read) and move to its right child for the round (go back to step 1).

Pseduo Code

PreorderWithMorrisTraversal(root)
  Let L be an empty list
  curr := root

  while curr != null
    if curr.left == null
      L.add(curr.val)
      curr = curr.right
    else
      pred = curr.left
      while pred.right != null and pred.right != curr
        pred = pred.right

      if pred.right == null
        L.add(curr.val)
        //1. link the current node to its inorder predecessor
        pred.right = curr
        curr = curr.left
      else
        //2. restore tree structure
        pred.right = null
        curr = curr.right

  return L

Preorder Traversal